C05 : Modéliser des actions mécaniques

Cours

Modèle global d'une action mécanique

La modélisation locale des AM est très lourde à manipuler. Pour passer du modèle local au modèle global d'une action mécanique, il suffit de faire la somme (par intégration) des actions mécaniques élémentaires.

Répartition linéique d'effort

Soien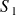t et 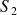deux solides en contact linéique le long d'une ligne 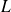, sur laquelle s'exerce l'action mécanique de 2 sur 1.

On doit s'intéresser d'abord à l'action mécanique transmise localement, sur une ligne élémentaire (tronçon 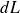de la ligne ).

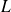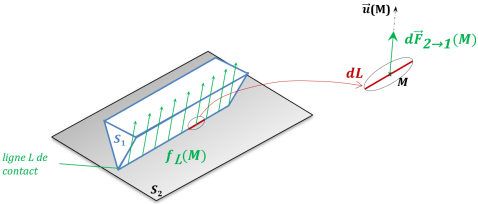
Élément considéré : ligne élémentaire

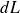
L'AM élémentaire de 2 sur 1 en un point M est modélisée par :
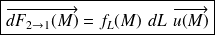
Elle est toujours orientée de 2 vers 1 pour ne pas rompre le contact.

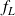: densité linéique d'effort (en 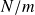), pouvant dépendre du point M dans le cas d'une répartition non uniforme.

L'action mécanique globale, résultant de ce contact s'écrit, en un point A quelconque :

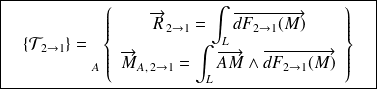
$\boxed{\quad \{ \mathcal T_{2 \rightarrow 1} \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{A} \left \{ \begin{array}{c} \overrightarrow{R}_{2\rightarrow 1} =\displaystyle\int_{L}\overrightarrow{dF_{ 2\rightarrow 1}(M)}\\ \overrightarrow{M}_{A, \,2\rightarrow 1}=\displaystyle\int_{L} \overrightarrow{AM}\wedge \overrightarrow{dF_{ 2\rightarrow 1}(M)} \end{array} \right \} \quad}$

Dans le cas particulier de l'action d'un contact entre deux solides sans frottement, la force élémentaire s'exerçant sur 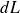s'écrit :

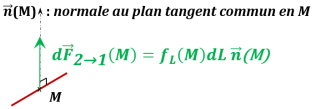
Répartition surfacique d'effort

Soien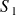t et 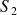deux solides qui possèdent une surface S commune, sur laquelle s'exerce l'action mécanique de contact de 2 sur 1.

On doit s'intéresser d'abord à l'action mécanique transmise localement, sur une surface élémentaire 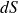, puis l'intégrer sur la surface 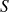du solide.

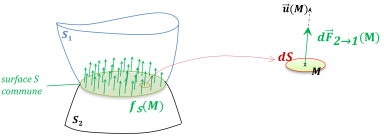
Élément considéré : surface élémentaire
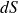
L'AM élémentaire de 2 sur 1 est modélisée par :
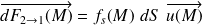
Elle est toujours orientée de 2 vers 1 pour ne pas rompre le contact.
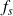: densité surfacique d'effort ou pression surfacique (en 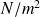), pouvant dépendre du point M dans le cas d'une répartition non uniforme.

L'action mécanique globale, résultant de ce contact s'écrit, en un point A quelconque :

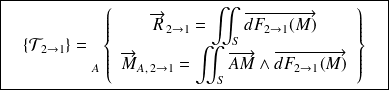
$\boxed{\quad \{ \mathcal T_{2 \rightarrow 1} \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{A} \left \{ \begin{array}{c} \overrightarrow{R}_{2\rightarrow 1} =\displaystyle\iint_{S} \overrightarrow{dF_{ 2\rightarrow 1}(M)}\\ \overrightarrow{M}_{A, \,2\rightarrow 1}=\displaystyle\iint_{S} \overrightarrow{AM}\wedge \overrightarrow{dF_{ 2\rightarrow 1}(M)} \end{array} \right \} \quad}$

Dans le cas particulier de l'action d'un fluide non visqueux sur un solide, ou d'un contact entre deux solides sans frottement, la force élémentaire s'exerçant sur 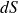s'écrit :

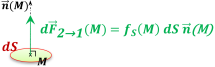
La force élémentaire est normale à la surface et fait intervenir la pression de contact 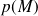(en 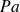). De manière générale, la pression n'est pas uniforme et dépend du point 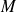considéré. De même, sauf dans le cas d'un contact plan, la normale au contact 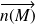dépend également du point M considéré.

L'action globale s'écrit, en un point 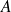quelconque :

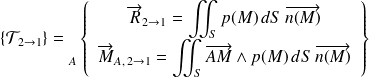
$\{ \mathcal T_{2 \rightarrow 1} \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{A} \left \{ \begin{array}{c} \overrightarrow{R}_{2\rightarrow 1} =\displaystyle\iint_{S} p(M)\,dS \, \overrightarrow{n(M)}\\ \overrightarrow{M}_{A, \,2\rightarrow 1}=\displaystyle\iint_{S} \overrightarrow{AM}\wedge p(M)\,dS \, \overrightarrow{n(M)} \end{array} \right \}$

Pour pouvoir conduire les calculs et obtenir le modèle global, il faut (cf TD) :

connaître la répartition de pression sur la surface de contact : uniforme, linéaire, etc...

déterminer la normale au contact ;

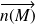déterminer l'expression de l'élément d'intégration .

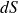Répartition volumique d'effort

On appelle action à distance toute action qui s'applique sur un système matériel S sans contact (action de la pesanteur, actions électromagnétiques, actions électrostatiques...).

Nous nous limiterons au cas des solides homogènes (masse volumique 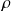constante).

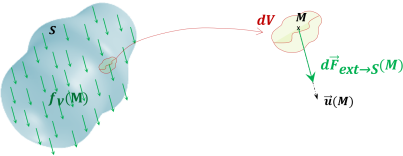
Élément considéré : volume élémentaire
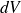
L'AM élémentaire à distance de l'extérieur sur S est modélisée par :
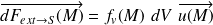
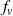: densité volumique d'effort (en 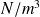), pouvant dépendre du point M dans le cas d'une répartition non uniforme.

L'action mécanique globale s'écrit, en un point 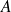quelconque :

$\boxed{\quad \{ \mathcal T_{ext \rightarrow S} \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{ext\rightarrow S}} \\ \overrightarrow{M_{A} (2\rightarrow S)} \end{array}\right\}}} _{A} \left \{ \begin{array}{c} \overrightarrow{R}_{ext\rightarrow 1} =\displaystyle\iiint_{V} \overrightarrow{dF_{ ext\rightarrow S}(M)}\\ \overrightarrow{M}_{A, \,ext\rightarrow 1}=\displaystyle\iiint_{V} \overrightarrow{AM}\wedge \overrightarrow{dF_{ ext\rightarrow S}(M)} \end{array} \right \} \quad}$

Exemple : Cas particulier de la pesanteur

Soit un solide S soumis à l'action mécanique de pesanteur.

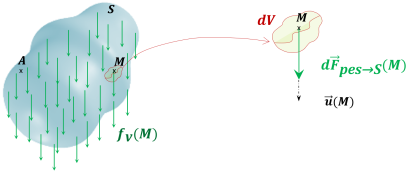
Un élément de volume 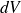subit une force élémentaire telle que :

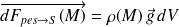
En supposant de plus que le solide est homogène, 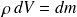et donc :

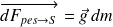
La résultante de l'action de pesanteur sur S est telle que :

$\overrightarrow{R}_{pes\rightarrow S}=\displaystyle\iiint_V \overrightarrow{dF_{pes\rightarrow S}} = \iiint_V \vec g\,dm=\vec g \iiint_V dm=m\,\vec g$

Le moment de l'action de la pesanteur sur 1 au point A s'écrit :

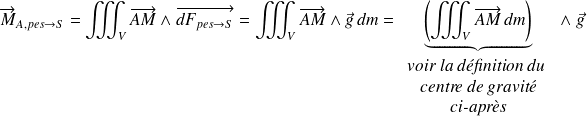
$\overrightarrow{M}_{A,pes\rightarrow S}=\displaystyle\iiint_V \overrightarrow{AM} \wedge \overrightarrow{dF_{pes\rightarrow S}} =\iiint_V \overrightarrow{AM} \wedge \vec g\,dm=\underbrace{\left(\iiint_V \overrightarrow{AM} \,dm\right)}_{\begin{array}{c}\textit{voir la définition du }\\\textit{centre de gravité}\\\textit{ci-après}\end{array}} \wedge \;\vec g$

D'où l'expression du moment :

$\overrightarrow{M}_{A,pes\rightarrow S}=m \,\overrightarrow{AG} \wedge \vec g$

On peut remarquer que ce moment est nul s'il est exprimé au point G :

$\overrightarrow{M}_{G,pes\rightarrow S}=m \, \overrightarrow{GG} \wedge \vec g=\vec 0$

Le torseur d'action de la pesanteur est donc un glisseur :

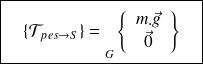
$\boxed{ \quad \{ \mathcal T_{pes \rightarrow S} \} = {\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}} _{G} \left \{ \begin{array}{c}m.\vec g \\\vec 0 \end{array} \right \} \quad }$

On retrouve ainsi le résultat donné au chapitre III. On peut de la même façon redémontrer les torseurs des actions mécaniques usuelles à partir des répartitions volumiques ou surfacique d'effort.

Définition : Centre de gravité

Le centre de gravité d'un solide est défini par la relation suivante :

$\boxed{ \quad\forall A, \quad\overrightarrow{AG}=\frac 1 m \iiint_V{\overrightarrow{AM} \, dm} \quad }$

Accueil

Imprimer