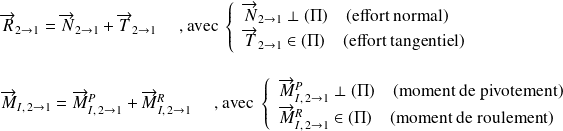C05 : Modéliser des actions mécaniques

Cours

Introduction

Soient deux solides 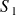et 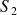en contact en un point 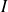. Soit ( 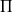) le plan tangent commun en I à 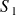et .

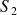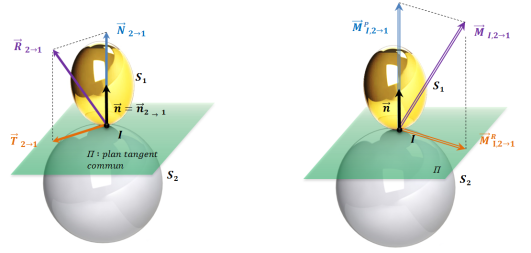
Afin de prendre en compte la résistance du solide 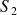à la rotation du solide 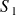, on modélise l'action mécanique de contact de 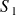sur 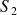au point 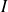par le torseur ( 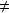glisseur):

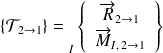
$\{ \mathcal T_{2 \rightarrow 1} \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{I} \left \{ \begin{array}{c} \overrightarrow{R}_{2\rightarrow 1} \\ \overrightarrow{M}_{I, \,2\rightarrow 1} \end{array} \right \}$

Soit 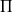le plan tangent commun aux deux solides au point I. On pose :

$\overrightarrow{R}_{2\rightarrow 1} =\overrightarrow{N}_{2\rightarrow 1} +\overrightarrow{T}_{2\rightarrow 1} \quad \text{ , avec } \left\{\begin{array}{l} \overrightarrow{N}_{2\rightarrow 1} \perp (\Pi) \quad\text{(effort normal)}\\ \overrightarrow{T}_{2\rightarrow 1} \in (\Pi) \quad\text{(effort tangentiel)}\end{array}\right. \\\\\\ \overrightarrow{M}_{I, \,2\rightarrow 1}=\overrightarrow{M}_{I, \,2\rightarrow 1}^P+\overrightarrow{M}_{I, \,2\rightarrow 1}^R \quad \text{ , avec } \left\{\begin{array}{l} \overrightarrow{M}_{I, \,2\rightarrow 1}^P \perp (\Pi)\quad\text{(moment de pivotement)}\\ \overrightarrow{M}_{I, \,2\rightarrow 1}^R\in (\Pi)\quad\text{(moment de roulement)} \end{array}\right.$

Accueil

Imprimer