Résistance au pivotement
La résistance au pivotement génère un moment en I qui s'oppose au pivotement du solide
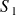 par rapport à
par rapport à
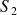 si
si
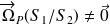 ou la la tendance au pivotement de
ou la la tendance au pivotement de
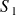 sur
sur
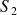 si
si
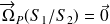
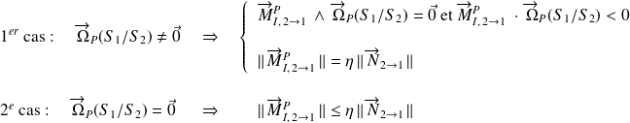
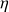 est le paramètre de résistance au pivotement. Il est homogène à une longueur (en
est le paramètre de résistance au pivotement. Il est homogène à une longueur (en
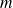 ).
).
Matériaux en contact |
|
|---|---|
Acier trempé sur acier trempé | 0,005 à 0,01 |
Fonte grise sur acier trempé | 0,5 |
Pneu sur sol en bon état | 5 à 20 |







