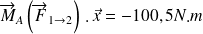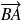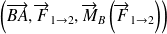Moment d'une force en un point
Mise en évidence : serrage d'une vis à l'aide d'une clé plate
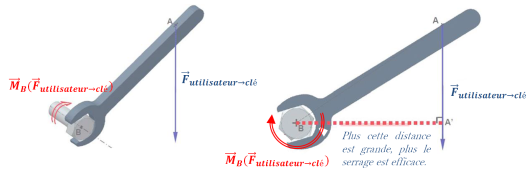
On considère l'action mécanique d'un utilisateur sur une clé modélisable par le vecteur force
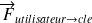, appliqué au point A.
Cette force aura tendance à faire tourner la vis permettant ainsi le serrage (ou desserrage).
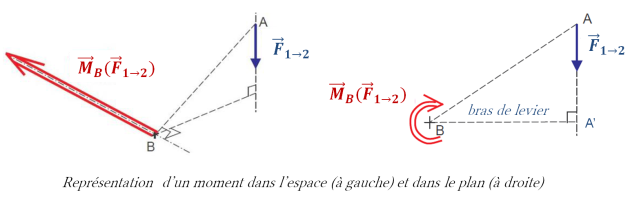
On dit alors que la force exercée au point A crée un moment au point B. Ce moment :
s'exerce autour d'un axe (celui de de la vis) : point d'application et direction ;
possède un sens (serrage ou desserrage) ;
possède une intensité.
Ainsi le moment d'une force peut être modélisé mathématiquement par un vecteur : le vecteur moment au point B noté
.
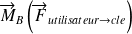La norme du vecteur moment correspond à l'intensité de la tendance à faire tourner la vis. Elle s'exprime en N.m et dépend :
de la norme de la force exercée sur la clé ;
de la distance BA' appelée « bras de levier » (avec A' projeté orthogonal de B sur le support de la force).
Expression du moment d'une force en un point
Fondamental :
On appelle moment au point B de la force
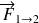appliquée en A le vecteur
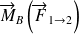tel que :
Ce moment s'exprime en Newton mètre (
)
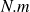Remarque :
1. Point d'application :
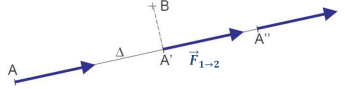
Si le point d'application de A de la force se déplace sur le support de celle-ci noté
, le moment ne change pas.
2. Direction : La direction du moment est orthogonale au plan formé par
3. Sens : Le sens du moment est tel que le trièdre
|  |
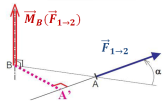4. Norme :
La norme du moment vaut :
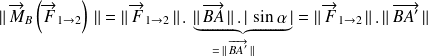
C'est à dire :
5. Cas de nullité :
Le moment en B est nul si :
la force
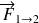est nulle ;
si le support de la force
passe par le point B, c'est à dire si le bras de levier est nul.
Conclusion :
Dans des cas simples, on pourra donner directement l'expression du vecteur moment en utilisant la formule suivante :
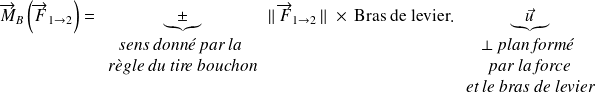
Dans les autres cas, on utilisera la définition avec le produit vectoriel :
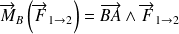
Complément : quelques ordres de grandeur de moments
Porte que vous fermez : moins de
.
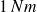Clé allen quand vous serrez une vis CHc :
.
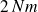Desserrage d'un écrou de roue de voiture : autour de
.
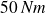Moment d'une force par rapport à un axe
On appelle moment d'une force
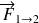par rapport à un axe
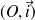la composante suivant
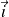du moment de la force en un point quelconque de l'axe
.
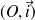Autrement dit, on calcule le moment en un point de l'axe, puis on projette ou on lit la coordonnée qui se trouve sur l'axe en question.
Exemple :
L'action du pied 1 sur la pédale 2 est représentée en M par une force
.
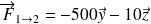On donne :
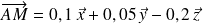(en m)
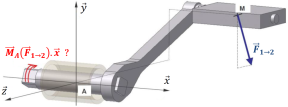
Objectif : calculer le moment de la force
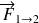par rapport à l'axe
.
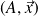Méthode 1 : Utilisation du produit vectoriel
Moment au point A de la force appliquée en M :
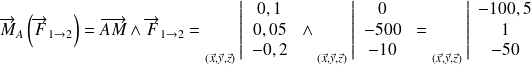
Ainsi, le moment par rapport à l'axe
est donc de
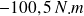
Méthode 2 : Utilisation du bras de levier
On représente ce qui se passe dans le plan perpendiculaire à l'axe
.
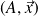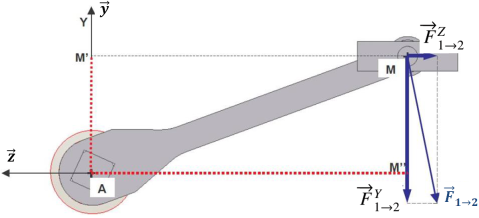
On décompose la force :
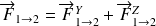
La composante
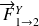exerce un moment en A égal, à :
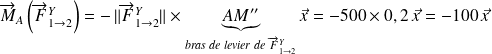
De même, la composante
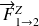exerce un moment en A égal à :
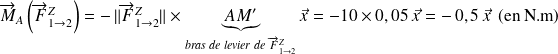
D'où le moment de
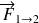autour de l'axe
:
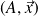