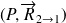C05 : Modéliser des actions mécaniques

Cours

Torseur d'une action mécanique transmissible

Nous venons de mettre en évidence le fait que deux vecteurs sont nécessaires pour modéliser convenablement une action mécanique s'exerçant sur un système matériel. En effet, selon le point où l'on se place pour ressentir les effets d'une action mécanique, un vecteur force et/ou un vecteur moment sont nécessaires.

Définition

Fondamental :

Le vecteur force et le vecteur moment en un point sont regroupés dans un torseur appelé torseur des actions mécaniques transmissibles :

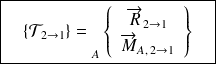
Ce torseur représente l'action mécanique de 2 (solide, liquide, gaz) sur un solide 1 :

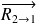: Résultante du torseur, vecteur indépendant du point où le torseur est exprimé (invariant vectoriel).
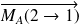: Moment du torseur, ce vecteur dépend du point d'expression du torseur.

Comme en cinématique, on peut utiliser les notations en ligne ou en colonne des torseurs faisant intervenir les composantes de chaque vecteur :

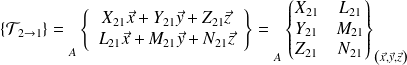
$\{ \mathcal T_{2 \rightarrow 1} \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{A} \left \{ \begin{array}{c} X_{21}\vec x +Y_{21}\vec y+Z_{21}\vec z \\ L_{21}\vec x +M_{21}\vec y+N_{21}\vec z \\ \end{array} \right \} = {\vphantom{ \left \{ \begin{matrix} X_{21} & L_{21} \\ Y_{21} & M_{21} \\ Z_{21} & N_{21} \\ \end{matrix} \right \} }} _{A} \left \{ \begin{matrix} X_{21} & L_{21} \\ Y_{21} & M_{21} \\ Z_{21} & N_{21} \\ \end{matrix} \right \}_{\left( \vec x, \vec y, \vec z \right)}$

Propriétés

Changement de point d'un torseur d'action mécanique

Connaissant le modèle de l'action mécanique de 2 sur 1 en un point A :

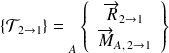
$\{ \mathcal T_{2 \rightarrow 1} \}={\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}}_{A}\left \{ \begin{array}{c}\overrightarrow{R}_{2\rightarrow 1} \\\overrightarrow{M}_{A, \,2\rightarrow 1}\end{array} \right \}$

il est possible de donner le modèle de cette action en un point B en utilisant la formule de changement de point du torseur :

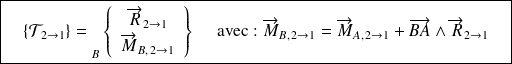
$\boxed{\quad \{ \mathcal T_{2 \rightarrow 1} \}= {\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R}_{2\rightarrow 1} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}}_{B} \left \{ \begin{array}{c}\overrightarrow{R}_{2\rightarrow 1} \\\overrightarrow{M}_{B, \,2\rightarrow 1}\end{array} \right \} \quad \text{ avec : } \overrightarrow{M}_{B, \,2\rightarrow 1}=\overrightarrow{M}_{A, \,2\rightarrow 1}+\overrightarrow{BA} \wedge \overrightarrow{R}_{2\rightarrow 1} \quad}$

Somme de deux torseurs

Le torseur représentant l'action de deux solides 2 et 3 sur un solide 1 peut s'écrire :

$\boxed{\quad \left\{ \mathcal T_{\{2+3\} \rightarrow 1} \right\}=\left\{ \mathcal T_{2 \rightarrow 1} \right\}+\left\{\mathcal T_{3 \rightarrow 1} \right\} \quad}$

Attention :

Pour pouvoir additionner les composantes de deux torseurs, ceux-ci doivent être réduits en un même point.

Torseurs particuliers

Torseur à résultante : glisseur

Fondamental :

Un torseur est un glisseur s'il existe un point P où le moment est nul.

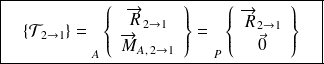
$\boxed{ \quad\{ \mathcal T_{2 \rightarrow 1} \}={\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}}_{A}\left \{ \begin{array}{c}\overrightarrow{R}_{2\rightarrow 1} \\\overrightarrow{M}_{A, \,2\rightarrow 1}\end{array} \right \}={\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}}_{P}\left \{ \begin{array}{c}\overrightarrow{R}_{2\rightarrow 1} \\\vec 0\end{array} \right \} \quad}$

Remarque :

Un glisseur est utilisé pour modéliser une force. Ses éléments de réduction restent identiques en tout point du support de cette force, soit en tout point de la droite

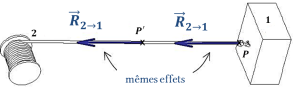Preuve :

Torseur couple

Fondamental :

Un couple est un torseur dont la résultante est nulle.

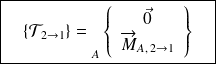
Exemple : Couple de forces

Soient deux actions mécaniques exercées par chacune des mains d'un utilisateur aux extrémités d'une clé, modélisables par deux glisseurs en B et en C :

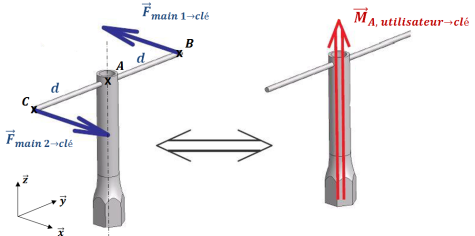
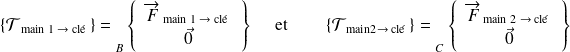
$\quad\{ \mathcal T_{\text{ main 1 }\rightarrow \text{ clé }} \} = {\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}} _{B} \left \{ \begin{array}{c}\overrightarrow{F}_{\text{ main 1 }\rightarrow \text{ clé }} \\ \vec 0\end{array} \right \} \quad \text{ et } \quad \quad\{ \mathcal T_{\text{ main2}\rightarrow \text{ clé }} \} ={\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}} _{C} \left \{ \begin{array}{c}\overrightarrow{F}_{\text{ main 2 }\rightarrow \text{ clé }} \\ \vec 0\end{array} \right \}$

Dans le cas où les deux forces 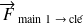et 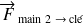ont même direction, même norme et sont de sens opposés on parle de couple de forces :

$\overrightarrow{F}_{\text{ main 2 }\rightarrow \text{ clé }} = -\,\overrightarrow{F}_{\text{ main 1 }\rightarrow \text{ clé }}=F\,\vec x, \quad \text{ avec } \quad F=\Vert \overrightarrow{F}_{\text{main 1}\rightarrow \text{ clé }}\Vert=\Vert \overrightarrow{F}_{\text{main 2}\rightarrow \text{ clé }}\Vert$

Et donc la résultante des actions mécaniques exercées par l'utilisateur sur la clé est nulle :

$\overrightarrow{R}_{\text{ untilisateur }\rightarrow \text{ clé }}=\overrightarrow{F}_{\text{ main 2 }\rightarrow \text{ clé }} + \,\overrightarrow{F}_{\text{ main 1 }\rightarrow \text{ clé }}=F\,\vec x - F\,\vec x =\vec 0$

De plus, les moments au point A de chacune de ces forces sont identiques :

$\overrightarrow{M_{A} (\overrightarrow{F}_{\text{ main 1 }\rightarrow \text{ clé }})}=\overrightarrow{M_{A} (\overrightarrow{F}_{\text{ main 2 }\rightarrow \text{ clé }})}= +\, F.d \, \vec z$

Donc le moment résultant des actions mécaniques exercées par l'utilisateur sur la clé correspondant à la somme des moments exercés par chacune des mains sur la clé s'écrit :

$\overrightarrow{M}_{A, \text{ utilisateur }\rightarrow \text{ clé }} = \overrightarrow{M_{A} (\overrightarrow{F}_{\text{ main 1 }\rightarrow \text{ clé }})} + \overrightarrow{M_{A} (\overrightarrow{F}_{\text{ main 2 }\rightarrow \text{ clé }})}= 2\, F.d \, \vec z$

On peut ainsi donner le torseur résultant de l'action mécanique de l'utilisateur sur la clé :

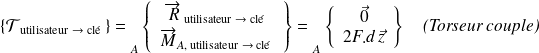
$\{ \mathcal T_{\text{ utilisateur }\rightarrow \text{ clé }} \} = {\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}} _{A} \left \{ \begin{array}{c}\overrightarrow{R}_{\text{ utilisateur }\rightarrow \text{ clé }} \\ \overrightarrow{M}_{A, \text{ utilisateur }\rightarrow \text{ clé }} \end{array} \right \}= {\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}} _{A} \left \{ \begin{array}{c}\vec 0 \\ 2F.d \, \vec z \end{array} \right \} \quad \textit{(Torseur couple)}$

Remarque :

Un torseur couple a les mêmes éléments de réduction en tout point de l'espace.

Preuve :

Accueil

Imprimer