C05 : Modéliser des actions mécaniques

Cours

Dualité torseurs d'actions mécaniques/cinématiques

On peut remarquer que dans le cadre des liaisons parfaites :

pour chaque degré de liberté supprimé, il existe une composante d'action mécanique susceptible d'être transmise par la liaison ;

réciproquement, aucune composante d'action mécanique ne peut être transmise là ou un mouvement relatif est possible.

Les torseurs d'actions mécaniques transmissibles et cinématiques sont donc liés : dans une direction donnée et en l'absence de frottement, soit le mouvement est possible, soit un effort peut être transmis. On parle de dualité entre le torseur cinématique et le torseur des actions mécaniques transmissibles.

Ainsi quelque soit la liaison considérée :

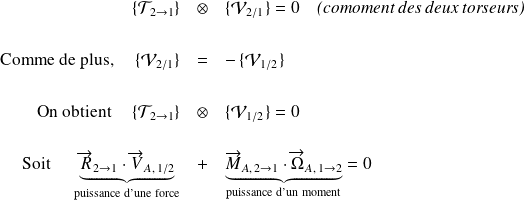
$\begin{eqnarray*} \{ \mathcal T_{2 \rightarrow 1} \} & \otimes & \{ \mathcal V_{2 /1} \} =0 \quad \textit{(comoment des deux torseurs)}\\ \\ \text{Comme de plus, } \quad \{ \mathcal V_{2 / 1} \} & = & -\,\{ \mathcal V_{1 / 2} \}\\ \\ \text{On obtient } \quad\{ \mathcal T_{2 \rightarrow 1} \} & \otimes & \{ \mathcal V_{1 / 2} \} =0 \\ \\ \text{Soit } \quad \underbrace{\overrightarrow{R}_{2\rightarrow 1} \cdot \overrightarrow{V}_{A, \,1/ 2}}_{\text{puissance d'une force} } & +& \underbrace{\overrightarrow{M}_{A, \,2\rightarrow 1} \cdot \overrightarrow{\Omega}_{A, \,1\rightarrow 2}}_{\text{puissance d'un moment} }=0 \end{eqnarray*}$

Autrement dit, la puissance dissipée par une liaison parfaite est nulle.

Accueil

Imprimer